Stochastic models for which only model simulation are available are increasingly being considered by practitioners and scientists in diverse fields. A crucial component to making these models more useful is to calibrate them to real data. Computational statisticians have been working hard on this parameter estimation problem for the past 15 years.
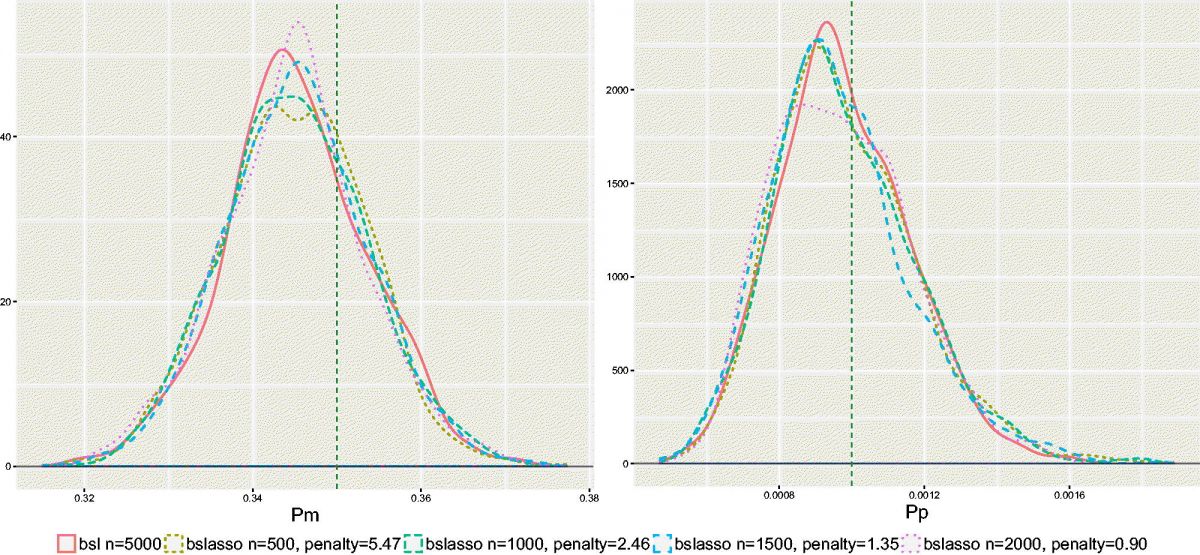
ACEMS researchers are continuing to build off their research into computationally efficient simulation-based parameter estimation methods for complex models. The foundation of their approach to parameter estimation for these models, called Bayesian synthetic likelihood, was published in 2018 in the Journal of Computational and Graphical Statistics [1]. For a wide class of models, their approach significantly reduces the computation time for parameter estimation and requires less practitioner intervention compared to the popular approximate Bayesian computation.
The research team remains heavily focussed on further computational enhancements. A follow-up paper just published in the same journal [2] manages to reduce further the number of model simulations required without sacrificing much on the accuracy of parameter estimates. Other work by the team [3,4] published in high-impact statistics journals allows models with a much larger number of parameters to be considered and massively reduces computational cost for applications where the data is very informative or high accuracy is not required.
- [1] https://amstat.tandfonline.com/doi/abs/10.1080/10618600.2017.1302882#.XK19w5gzZPY
- [2] https://www.tandfonline.com/doi/abs/10.1080/10618600.2018.1537928?journalCode=ucgs20
- [3] https://link.springer.com/article/10.1007/s11222-017-9773-3
- [4] https://www.sciencedirect.com/science/article/pii/S0167947318301749