The Function with a $1-Million Bounty on its Head

In 1859, the German mathematician Bernhard Riemann wrote a paper generating consequences that are still echoing almost 160 years later.

In it, he proposed an analysis of the prime numbers using a special function with seemingly mystical properties and now named after him: the Riemann zeta function. A famous hypothesis Riemann formulated about his function is considered so significant, for instance, that the Clay Mathematics Institute in the US has put up a bounty of US $1 million for anyone who can give a proof of it.

Now, Professor Peter Forrester, a Chief Investigator at the ARC Centre of Excellence for Mathematical and Statistical Frontiers (ACEMS) together with collaborators Dr Anthony Mays and Professor Folkmar Bornemann are adding to the legend by employing the Riemann zeta function in their quest to develop tools to analyse big data sets using analogies with physical systems.

The prime numbers are the building blocks of the integers—a sequence with perfect order—although they themselves occur seemingly at random. Quantifying the randomness of the primes as initiated by Riemann is perhaps the most famous unsolved problem in mathematics.

reimenn-forester.jpg

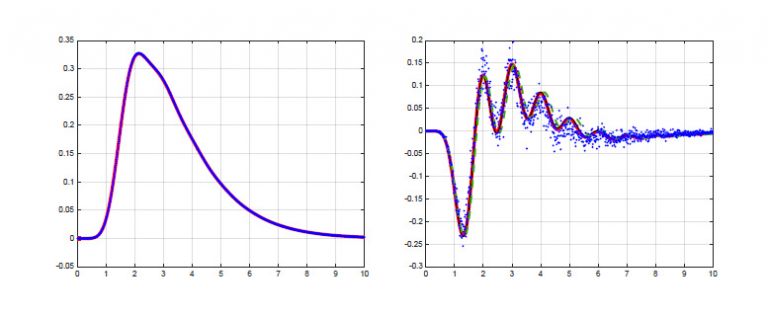
The first graph compares data to random matrix predictions. The statistical accuracy of the data set is so great that a structured difference can be extracted in the second graph. This difference also agrees with random matrix predictions.

Riemann analysed the primes using the zeros of the zeta function. In recent years it has emerged that the zeros behave like the energy levels of a quantum billiard system with chaotic dynamics. If this physical analogy could be proved true, the optimal randomness of the primes would follow, but at present there is only partial validation.

Peter, a professor in the School of Mathematics and Statistics at The University of Melbourne, is using an enormous database of more than one billion Riemann zeros generated by US mathematician and computer scientist Andrew Odlyzko to probe the quantum analogy. He has found unequivocal evidence for the hypothesis that the zeros and quantum energy levels have the same statistics, as the zeros get bigger. But the statistical accuracy provided by the dataset reveals more.

“It doesn’t only provide a measure of the limiting distribution, it even shows the approach—how you reach it,” Peter says.

More broadly, Peter and his collaborators are seeking analogies with physical systems as a method to analyse big and complex datasets, such as would be found in problems to do with logistics, transport and government decisions relating to health care and welfare systems.