Stock markets are difficult to model. Take for example, modelling the evolution of a stock option, a promise to buy or sell a stock at an agreed price sometime in the future. All you know are three things: the trend of the associated stock, where the market is in the economic cycle, and how the option price varies a function of the economic cycle and the stock.
The real difficulty is that the futures of all three dimensions are partly random and partly dependent on each other.

uoa_ai_dr_giang_nguyen.jpg
Dr Giang Nguyen
It’s one of a general set of problems that mix randomness and interdependence (known as stochastic fluid-fluid processes), with which Dr Giang Nguyen and colleagues including Chief Investigator Professor Nigel Bean from the University of Adelaide, are wrestling. Another example is the impact of bleaching on coral growth.
“These kinds of processes, because of the dependence between the dimensions, are difficult to analyse. It wasn’t until 2014 that Nigel and a colleague, Associate Investigator Dr Malgorzata O’Reilly from the University of Tasmania, devised a formula to describe the long-term behaviour of such systems, where they converged to an equilibrium,” says Giang, who is an Associate Investigator at the ARC Centre of Excellence for Mathematical and Statistical Frontiers (ACEMS). Unfortunately, their formula incorporated mathematical elements that were not easily computed.
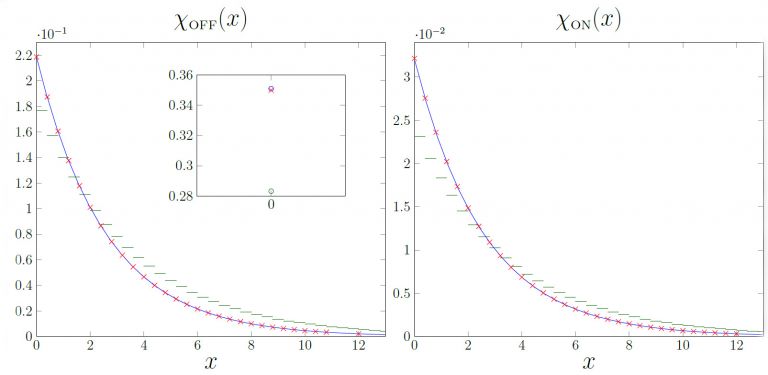
giang-nguyen-figures.jpg
Comparisons between exact densities (red crosses) and their approximations (blue and green curves) for various scenarios of a stochastic fluid-fluid process. The piecewise-linear approximation (blue curve) fit through all exact values, indicating that the approximation is highly accurate. The subplot inside the left plot shows the corresponding probability masses at value 0, where once again the piecewise-linear approximation (blue circle) takes the same value as the exact probability mass (red cross).
“We are turning the mathematical operators into matrices that computers can handle, and the approximations we’re producing look quite good. Right now, we can numerically evaluate the long-term behaviour of all three dimensions in such processes.”
What the ACEMS researchers need to do next is develop mathematical theory behind their methods, to prove analytically how their approximations are correct, so that their technique can be generalised across many problems.
The research has benefited from feedback from other researchers after Giang has presented it at conferences, which ACEMS gave her financial support to attend. For instance, after talking about her work at the Australian Mathematical Science Conference in Canberra in December 2016, she has recently received a relevant paper and suggestions on how she might proceed on the theoretical front from Professor Gary Froyland of the University of New South Wales. Giang also presented the research at the International Conference on Matrix Analytic Methods in Stochastic Models in Budapest in June 2016.


