lattice_reduction_and_invariant_measure.jpg
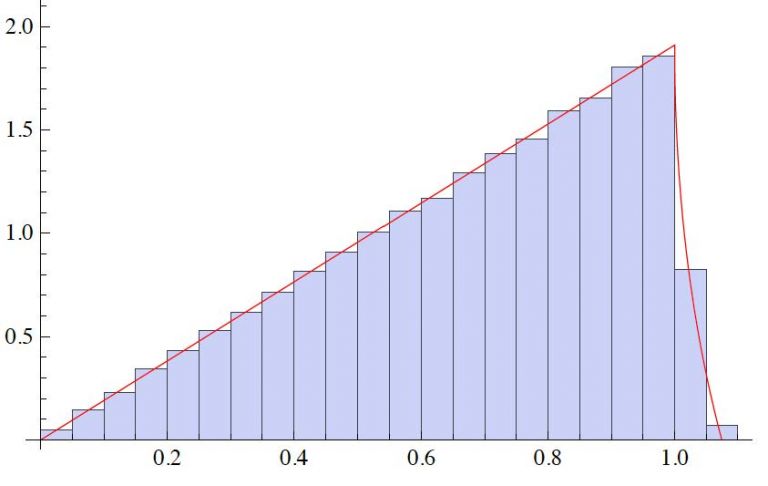
Comparison of numerically generated distribution for the magnitude of the shortest lattice vector in two dimensions for a basis chosen with invariant measure, and the theoretic prediction.

Comparison of numerically generated distribution for the magnitude of the shortest lattice vector in two dimensions for a basis chosen with invariant measure, and the theoretic prediction.