The knapsack problem is a classical mathematical problem that asks what is the optimal selection of items to place in a knapsack that maximises the total value of the filled knapsack, while ensuring that a weight or volume capacity constraint of the knapsack is not exceeded? It is easy to state, but quite challenging to solve, especially for large-scale practical applications such as those found in logistics, where the "knapsack" may be a shipping container or truck, or in finance where the "knapsack" may be a portfolio of shares that need to be chosen to maximise expected return while satisfying a budget constraint.
https://www.smithsonianmag.com/science-nature/why-knapsack-problem-all-around-us-180974333/
It may be obvious which items should be "clearly in" (low weight, high value) and which ones should be "clearly out" (high weight, low value). The challenge however is to devise algorithms that can efficiently crunch through all the combinations of the remaining "middle band" to find the most valuable and compact solution.
Algorithms for solving the knapsack problem have been proposed since the middle of last century but, like any optimisation problem, their success depends on the particular data (weights and values) of a given test instance. In the 1990s, interest turned to understanding what data properties make a test instance hard to solve, spurred on by the realisation that public key cryptography systems that involve solving an underlying knapsack problem (in particular, the Merkle-Hellman knapsack cryptosystem, proposed in 1978 and declared insecure in 1984) were vulnerable to attack if the knapsack problem was not hard enough.
In 2005, Danish researcher David Pisinger published a paper called "Where are the hard knapsacks?", criticising the existing benchmark test instances as too easy, and proposing a new set of more challenging test instances that incorporated correlation structures between the weights and values of items that made solution more difficult.
Around that same time, I began work on a powerful new methodology for visualising the strengths and weaknesses of algorithms, known as Instance Space Analysis. By constructing a 2D map that represents test instances as points, and calculates the mathematical boundary of all possible test instances, the instance space also reveals where the easy and hard instances lie in the space from the perspective of each algorithm. I presented the methodology at a conference in Montreal in 2007, and an audience member suggested that my ideas might provide an answer to Pisinger's question. I added it to my mental "to-do" list.
It wasn't until 2012, when I received an ARC Discovery grant to progress my Instance Space Analysis methodology, that I finally had the resources to recruit a team to help advance the methodology and demonstrate its success on a wide variety of optimisation problems, including the knapsack problem.
My honours student, Jeffrey Christiansen, took on the challenge in 2013, making some good progress understanding the difficulty of the knapsack problem and experimenting with how various features of the data impact algorithm performance. When Jeffrey commenced a PhD at another university in 2014, and I was awarded an ARC Laureate Fellowship to explore the application of Instance Space Analysis in other fields beyond optimisation, the knapsack problem moved to the back-burner. Over the next few years, the knapsack baton was passed on to a series of summer vacation students and undergraduate project students, each chipping away at the problem and experimenting with how to create harder instances.
It wasn't until Jeffrey finished his PhD in 2018 that I approached him again to see if he wanted to finish what he had started. Funded by my Laureate Fellowship, Jeffrey worked part-time with me and my postdoc, Mario Andrés Muñoz-Acosta, to go deeper into new ideas, and finally achieve our quest to create an instance space for the knapsack problem filled with the most comprehensive set of challenging and diverse test instances.
By the time Melbourne was in lockdown, there was nothing left to do but tell the story. By mid-2020 the long awaited paper was submitted, and as we emerged from lockdown at the end of 2020, it was finally accepted and shared online. Eight years in the making, and five years before that on a "to do" list, I have found it so rewarding to finally be able to share an answer to Pisinger's question "where are the hard knapsacks?"
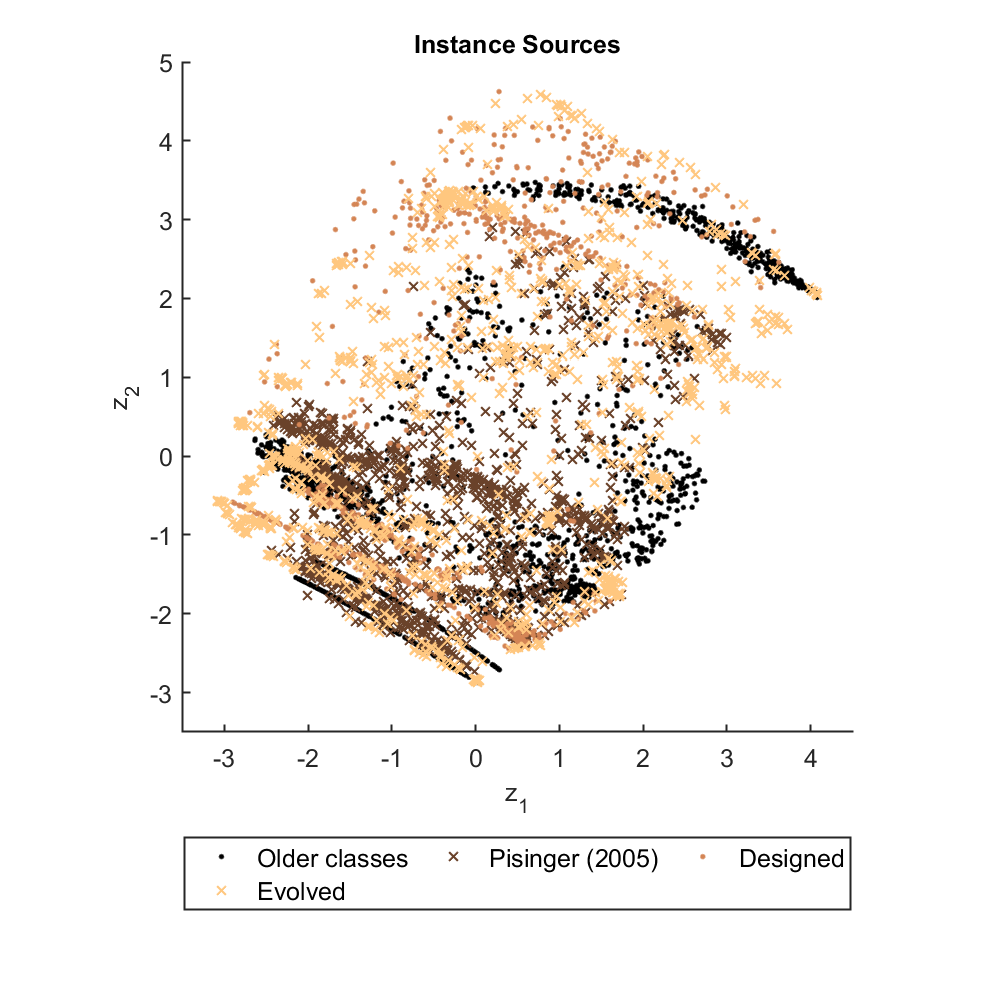
The answer lies in picture form: The classical instances that Pisinger criticised as "too easy" are shown in our Instance Space as black dots; Pisinger's 2005 "harder" instances are shown as brown crosses. My team has shown that the hardest instances lie in the bottom left of the instance space, and we have generated over one thousand new test instances (shown as beige dots and crosses using two methods) to explore the whole instance space, especially the hardest region. I just wish I could remember which researcher suggested in Montreal 14 years ago that we might be able to answer Pisinger's question so I could send them the answer!