
killa_warby_v17nth.png
The 16th Nigel Aylott Memorial Rogaine and 44th Victorian Rogaining Championship map (click to enlarge).
The sport of rogaining was invented in Australia during the 1970s and today is enjoyed worldwide. It involves long distance cross-country navigation over periods from 6 to 24 hours. Various controls or checkpoints are spread around the competition area and each is worth a certain number of points, usually varying from 20 to up to 100 points. For a 24 hour Championship event, the checkpoints could be spread around an area of approximately 200 square kilometres. Teams of 2 to 5 people have to visit checkpoints in such a way as to maximate their total number of points. Teams must start and finish at the home base, which in rogaining is called the Hash House. Maps wth checkpoint locations plotted are handed out three hours before the start for teams to plan their intended route. Courses are set so that the very best teams should just fall short of cleaning the course (i.e. visiting all checkpoints) making it a challenge to decide exactly what checkpoints to leave out. Most teams have a lower duration limit - they know they cannot cover more than a certain number of \(K\) cross-country kilometres under ideal conditions and may indeed fall short of this target.
Competition data
From the 2019 Victorian State Championship you are given:
- the coordinates (actually GPS latitude and longitude) \((x_{0}, y_{0})\) of the Hash House (checkpoint \(i_{0}\)) which must be the start and finish point of any route
- the ID numbers \( \{N_{i}\} \) of the 65 checkpoints;
- the coordinates \(\{(x_{i}, y_{i})\}\) of the 65 checkpoints;
- the point values \(\{M_{i}\}\) are given by the tens part of the ID number e.g. checkpoint 73 is worth 70 points, checkpoint 103 is worth 100 points.
Competition task
Find the number \(n\) of checkpoints and the sequence \(i_{1}, i_{2}, \ldots, i_{n}\) of check point IDs which satisies \\( \sum_{k = 1}^{n} d(i_{k-1}, i_{k}) + d(i_{n}, i_{0}) \leq K \\) and maximises \(\sum_{k = 1}^{n} M_{i_{k}} \), where \(d(N_{i}, N_{j})\) is the geodesic distance between the checkpoints.
If two routes have the same value of \(\sum_{k = 1}^{n} M_{i_{k}} \) then the shortest route is the best.
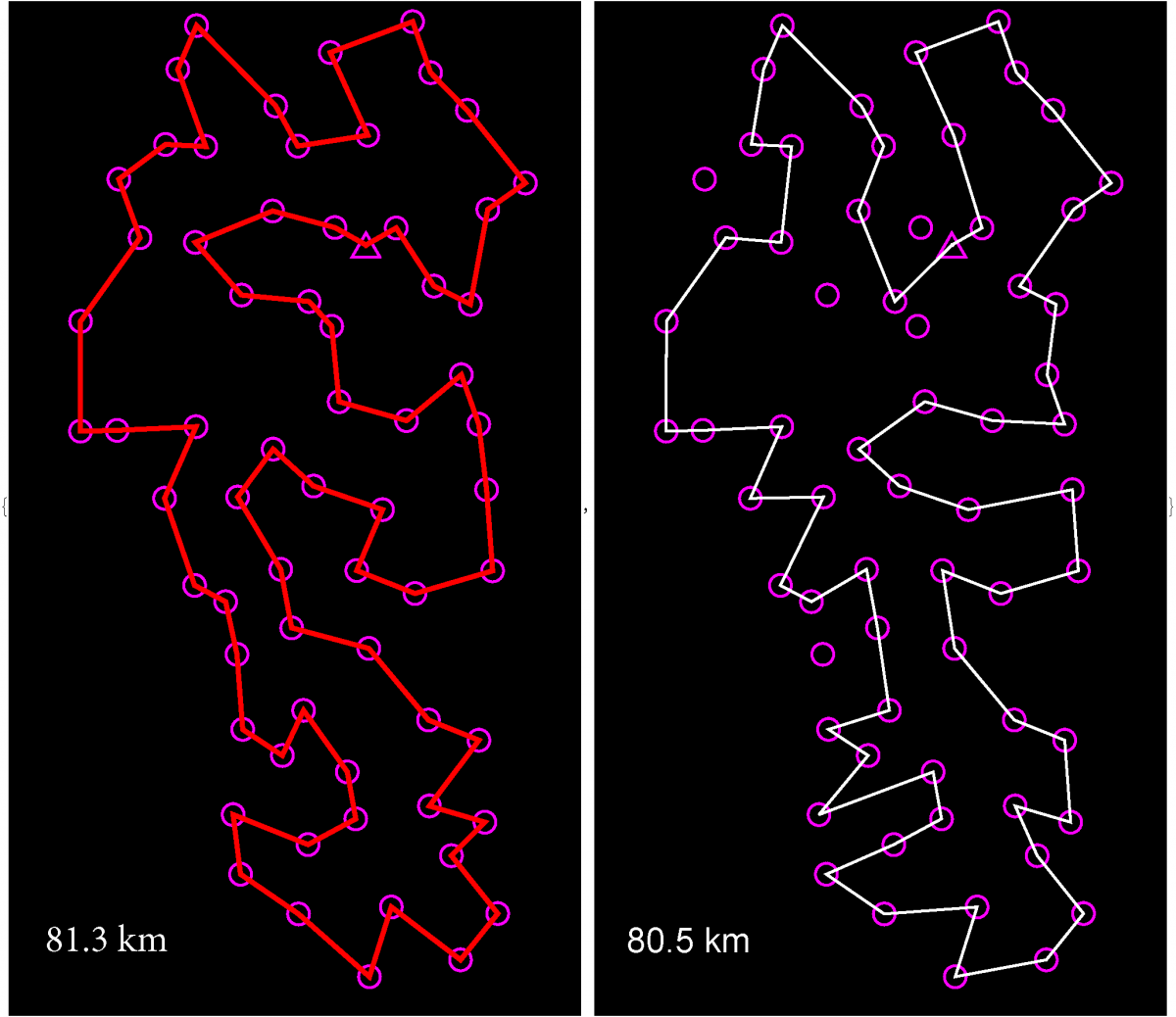
comparechampstooptimal.png
Left: The calculated shortest route to clean the course using the travelling salesman function in Mathematica. Right: Actual route traversed by State Champion team.
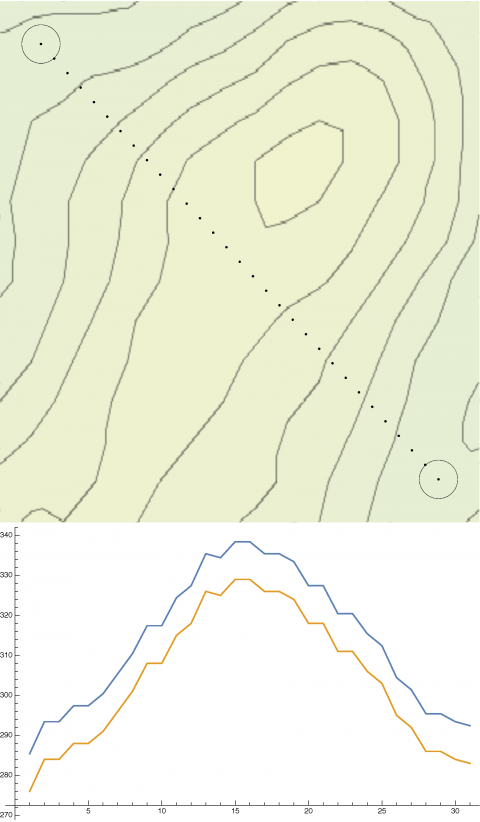
elevationexample.png
An example of differing elevation changes between checkpoints. (click to enlarge)
Competition requirements
- Entries should give optimal rogaine routes for \( K = 45, 55, 65, 75\) kms;
- the method of computation should be described (this may simply use standard existing software);
- the results should be presented graphically;
- entries with tied routes will be separated by the quality of the written and graphical presentation of the results, and any exploration of extensions;
- geodesic distance should use the WGS84 reference ellipsoid.
More realistic route choices
Simple "straight line" distrance between checkpoints is a very incomplete measure of overall leg difficulty. Rogainers take into account multiple factors in route planning, for example:
- topography;
- out-of-bounds areas;
- likely ground status on the leg e.g. vegetation density, rocky ground, fallen timber, presence of convenient walking tracks, etc.;
- creek/river crossings.
Precise elevation data is readily available for the course area. This could be used in various ways to directionally weight the baseline geodesic leg "lengths". The optimal tour could then be solved as an asymmetric tour on the complete checkpoint graph.
Awards
The competition is open to all students. Submissions are accepted from individuals and teams. The winning entry will receive a $1200 award. Second and third place receive $600 and $200, respectively.
Submissions
The deadline for submissions is 31 January 2020 (23:59:59, UTC-12). Winners will be announced in February 2020. Please upload your submission to https://acems.org.au/submission-form-optimal-rogaine-courses-competition.

warby-ovens_national_park.jpg
Collage of photos of the Warby-Ovens National Park near Wangaratta in northern Victoria - the location for the 2019 Victorian State Championship.
