It remains possibly the greatest unsolved problem in mathematics.
The Riemann hypothesis involving prime numbers has been around since 1859, but no one has ever proved it. There’s even a $1-million bounty for anyone who does prove it.

forrester-mays-web.jpg
Prof Peter Forrester & Dr Anthony Mays
“We’re happy to build on this. There is a mathematical heritage and so much interest in prime numbers, and trying to explain them,” said Prof Peter Forrester, an ACEMS Chief Investigator at The University of Melbourne.
Peter teamed up with his ACEMS' colleague at The University of Melbourne, Dr Anthony Mays, and Prof Folkmar Bornemann from the Technical University of Munich, to write the paper, “Finite Size Effects for Spacing Distributions in Random Matrix Theory: Circular Ensembles and Riemann Zeros”.
At the heart of the Riemann hypothesis is the Riemann zeta function, which tries to describe the distribution of prime numbers. But the function may have more than just mathematical properties.
In the 1980’s, the work of M.V. Berry at the University of Bristol showed how the Riemann zeroes could describe something in the physical world. In this case, the energy levels of quantum chaotic systems.
But there was a catch. It only held for infinitely large zeroes, which is theoretically meaningful but, in practice, inaccessible.
By the year 2000, J.P. Keating and N.C. Snaith, also from the University of Bristol, used random matrices to present a finite size model.
So now we’ve gone from prime numbers, to energy levels, to random matrices – all involving the Riemann zeta function.
“So now there are three links in this chain,” said Anthony.
It is in this third link, in the area of random matrices, that the ACEMS team was able to bring its expertise.
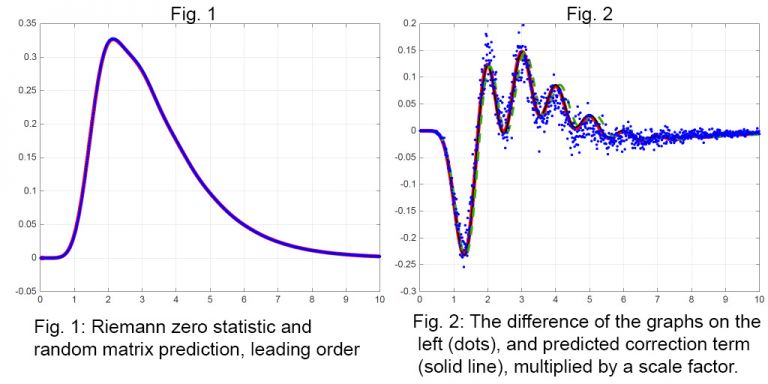
Their work dealt with a very big data set, due to A.M. Odlzyko, formerly from Bell Labs. In this case, a billion numbers starting at 1023. Despite the size of that number, it is not infinity. That means as you explore it, there will be corrections, or secondary effects.
“These secondary effects are essentially the fluctuations about the trend line. The trend line itself has been known for a long time, but if we can understand the fluctuations, then that gives us more information about the details of data, and helps us strengthen the connections,” said Anthony.
“Our paper actually makes use of a very high quality data set to analyse the secondary effects. For that to be possible, you need the data set and the theoretical developments within random matrix theory,” said Peter.
For Peter, dealing with big data and the Riemann zeta function has been the focus of his ACEMS research. But dealing with such a difficult problem, and a very large data set, is certainly no easy task.
“To probe these questions requires a deep understanding of theory, and it requires a computational side where we’re calculating quantities that haven’t been thought of,” said Peter.
In other words, their work really is a highlight – and is now getting some well-deserved recognition.
ACEMS media contact: Tim Macuga, 07 3138 6741, timothy.macuga@qut.edu.au