case study: Beyond the bell curve
What do traffic jams have to do with the way a coffee stain grows, or with matrices full of random numbers? When viewed from the right angle, all of them reveal a statistical curve known as the Tracy-Widom probability distribution.
"These phenomena appear to be very different, but the underlying mathematics is all the same," says Professor Jan de Gier, one of several ACEMS researchers fascinated by universality – the idea that certain mathematical structures occur again and again in apparently unrelated situations.
The study of universality began with the famous bell curve, the graph of the Gaussian or normal distribution that approximates the spread of independent variables like the heights in a crowd of people or the number of heads in a string of coin tosses.
"Tracy-Widom is another one of these universal distributions," says Jan. "More complicated, but still natural and ubiquitous."
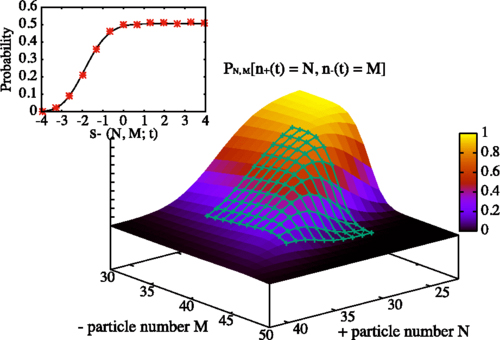
The Tracy-Widom distribution usually arises in systems of interacting particles or other objects, and until recently most mathematicians had studied situations where all the particles were of the same type.
In June 2018, however, Jan and PhD student Zeying Chen, together with collaborators from the Tokyo Institute of Technology, published the first exact mathematical description of a mixture composed of two types of particles that interact with one another and display a Tracy-Widom distribution.
"It's amazing how two things can seem to have nothing to do with each other and then all of a sudden – the same curve appears," says Jan.
The path to revealing the universality of the Tracy-Widom distribution travelled through physics as well as mathematics. Work by physicists studying systems such as interface growth of adsorbing atoms in the 1980s discovered similarities across a broad group of situations they called the KPZ universality class.
A decade later, mathematicians found that certain kinds of random matrices modelling atomic energy levels also fell into the KPZ class. Unlikely mathematical connections have continued to bloom, including to the Riemann zeta function and the distribution of prime numbers.
ACEMS researcher Professor Peter Forrester, who had been investigating applications to the energy levels of atomic nuclei, was one of the pioneers on the random matrix side of this research.
Michael Wheeler is also studying the KPZ universality class, and recently published an epic paper with renowned MIT mathematician Alexei Borodin that focuses on the movement of interacting particles on a lattice-like grid.
Studying universal distributions means that applications are everywhere. Jan has worked on more complex models of traffic flow with others including Dr Joyce Zhang and Associate Professor Tim Garoni, now at Monash University. Joyce and Tim have continued this work in cooperation with VicRoads, the Victorian road authority.
Tim is now also studying universality in statistical mechanics – the branch of mathematical physics that tries to understand the macroscopic world by modelling the behaviour of enormous numbers of tiny particles. Tim is working on the Ising model, a mathematical model of atoms that interact with their neighbours which provides fundamental insights into the behaviour of more complex real-world systems and how universal behaviour at macroscopic scales emerges from microscopic interactions.
Collaboration has been a key to all this research, Jan says. Not only among colleagues within ACEMS, but also with scholars elsewhere around the world.
His own recent work with Zeying Chen on the two-species Tracy-Widom distribution would not have come about without extended periods of time for collaboration with Professor Tomohiro Sasamoto and his student Iori Hiki from the Tokyo Institute of Technology. These get-togethers occurred at the Kavli Institute for Theoretical Physics in the US and at the ACEMS-backed MATRIX institute at Creswick in regional Victoria.
"Uninterrupted time and the space to cooperate and exchange ideas is vitally important," Jan says. "All this work is a result of worldwide collaborations."

Figure 1 – The AHR model. A+ (−) particle, denoted by filled circle (open circle), hops to the right (left) with rate β (α). A pair of + and − on neighboring sites swap their positions with rate 1.
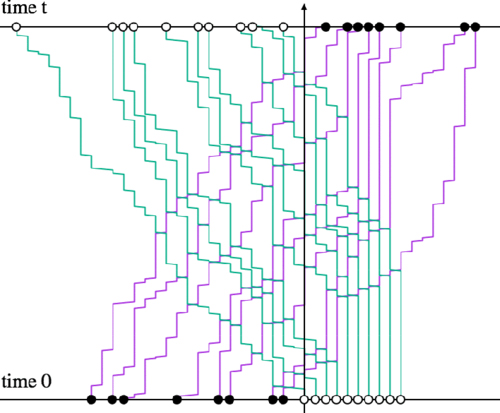
Figure 2 – The initial condition consisting of N+ particles (filled circle) with density ρ on the left and M−particles (open circle) packed on the right. In this Letter, we focus on the case of total exchange.